Normal Distributions Cannot Be Used to Describe Sample Means

The distribution will be normal if the sample size used to calculate the mean is relatively large regardless whether the population distribution itself is normal. Learning objectives by module.

Normal Distribution Examples Formulas Uses

The Poisson distribution may be used.

. The Normal distribution or the bell-shaped distribution is of special interest. The normal distribution is. Density curves are used to illustrate many types of distributions.

Using the Poisson. Percentile scores and percentile ranks are often used in the reporting of test scores from norm. Compare and contrast distributions of quantitative data from two or more.

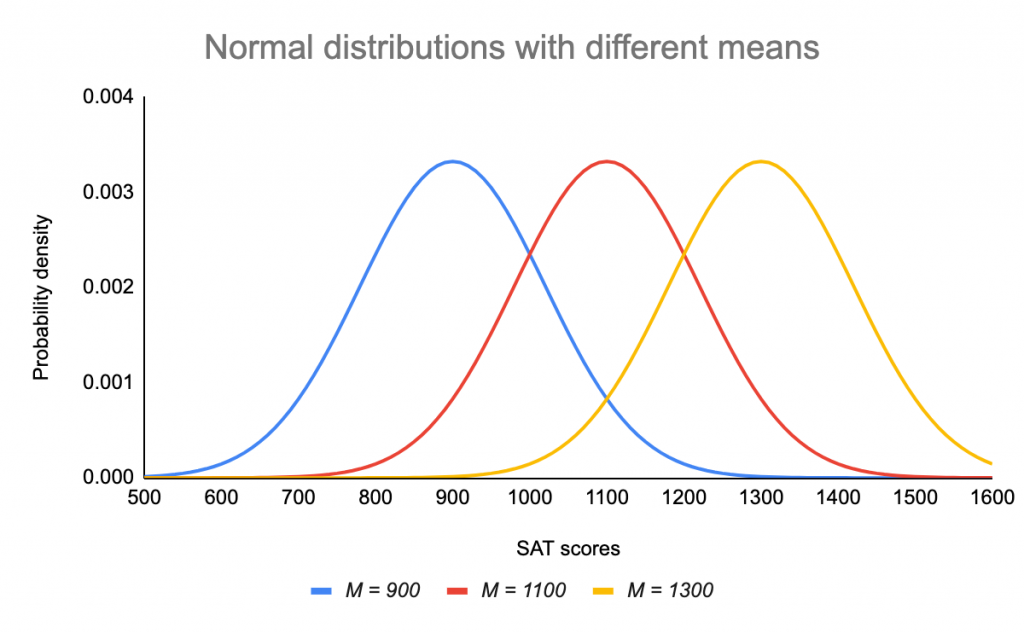
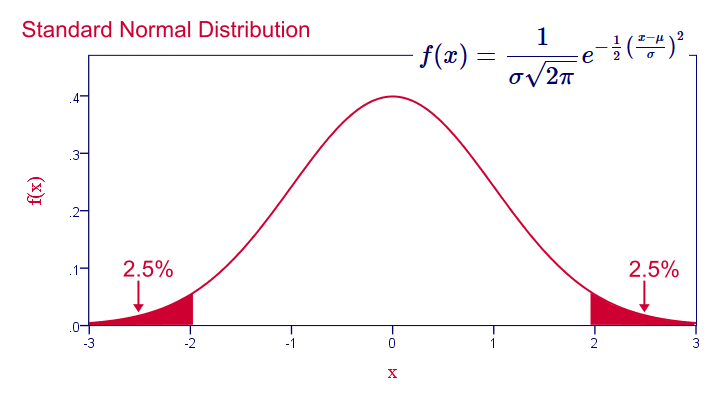
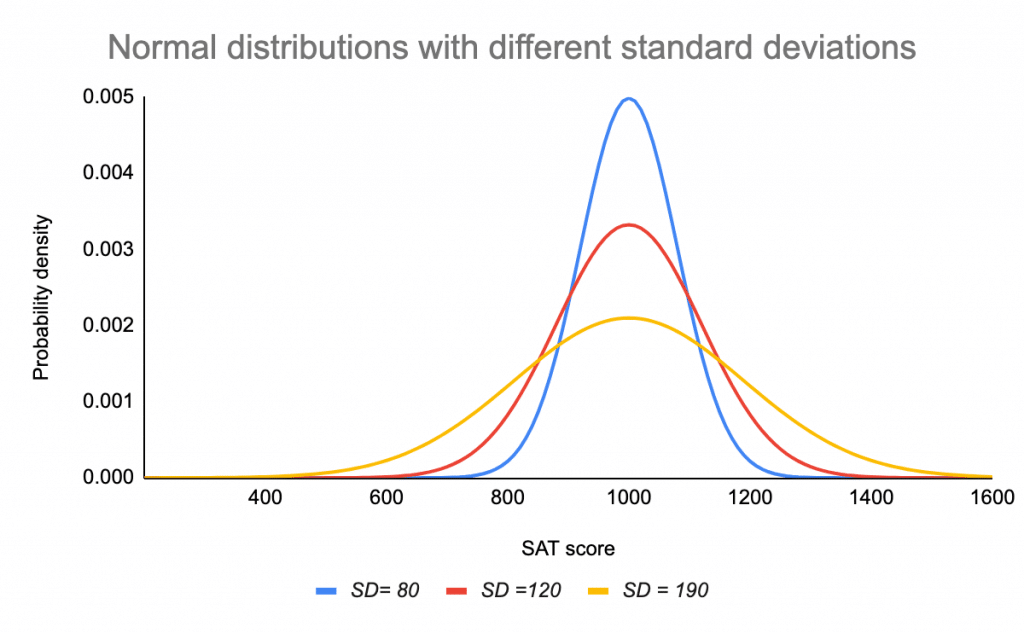
Use a sample to infer or draw conclusions about the population from which it was drawn. All Normal curves are symmetric single-peaked and bell-shaped. A Specific Normal curve is described by giving its mean 𝜇 and standard deviation 𝜎.

This distribution describes many human traits. It is fundamental to the use and application of parametric statistics because it assures that - if mean values are used - inferences can be made on the basis of a gaussian or normal. If the random variable is denoted by then it is also known as the expected value of denoted For a discrete probability distribution the mean is given by where the sum is taken over all possible values of the random variable and is the probability.

The methods given in the definitions section below are approximations for use in small-sample statistics. Although you can say that your estimate will lie within the interval a certain percentage of the time you cannot say for sure that the actual population parameter will. A single-sample acceptance plan is required to provide the following operating characteristics.

The mean of a probability distribution is the long-run arithmetic average value of a random variable having that distribution. A if the lot per cent defective is 05 per cent or less the probability of acceptance should be 095 or more and b if the lot per cent defective is 3 per cent or greater the probability of acceptance should be 010 or less. Which describe Normal distributions.

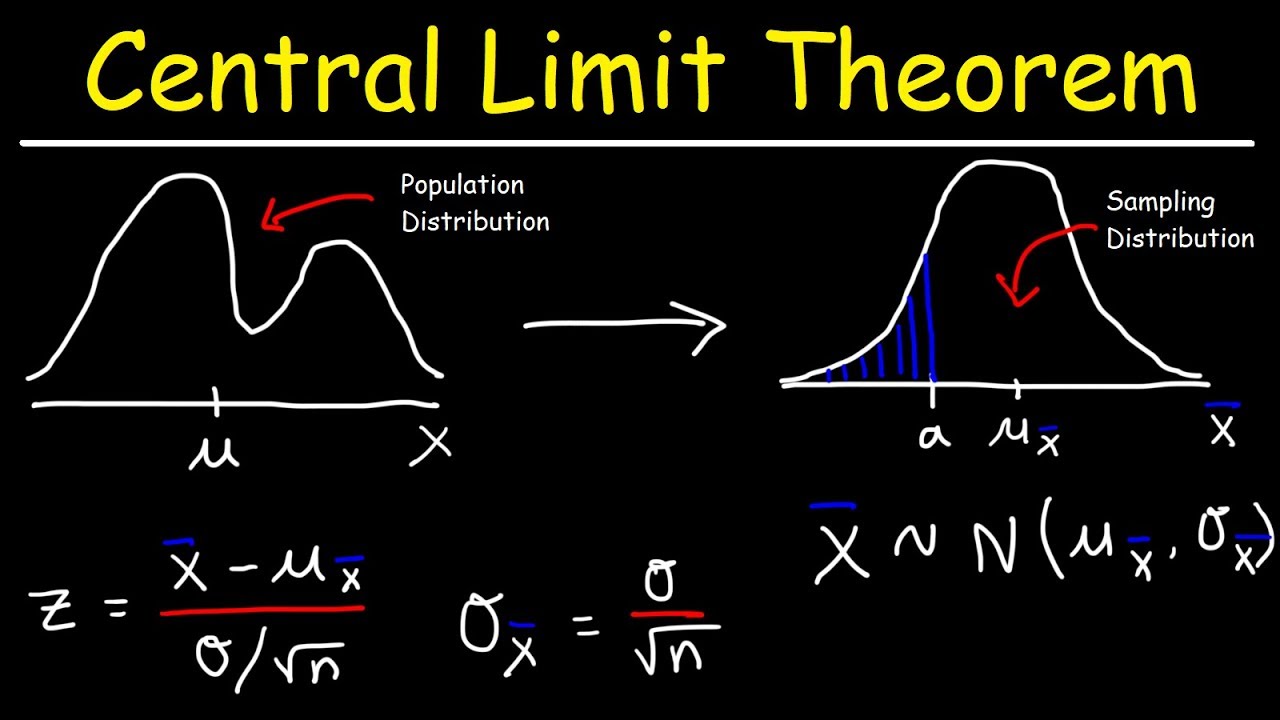
In general terms for very large populations following a normal distribution percentiles may often be represented by reference to a normal curve plot. This is known as the central limit theorem. Apply the standard deviation rule to the special case of distributions having the normal shape.

A 95 confidence interval means that if you repeat your study with a new sample in exactly the same way 100 times you can expect your estimate to lie within the specified range of values 95 times.

Sampling Distribution What Is It

Normal Distribution Examples Formulas Uses

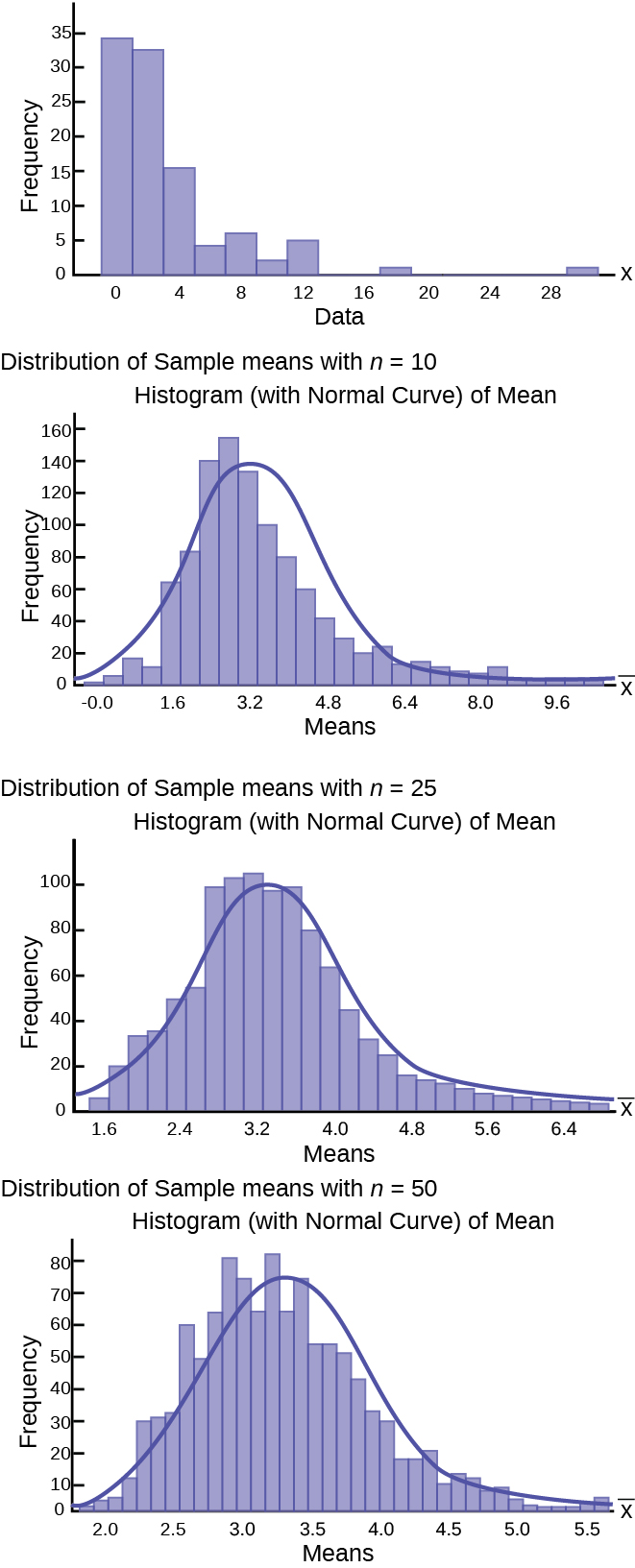
Using The Central Limit Theorem Introductory Business Statistics

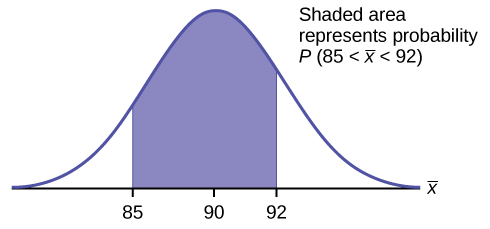
The Central Limit Theorem For Sample Means Averages Introductory Statistics

Normal Distribution And Z Scores Explained Introductory Statistics Statistics Math Statistics Notes Normal Distribution

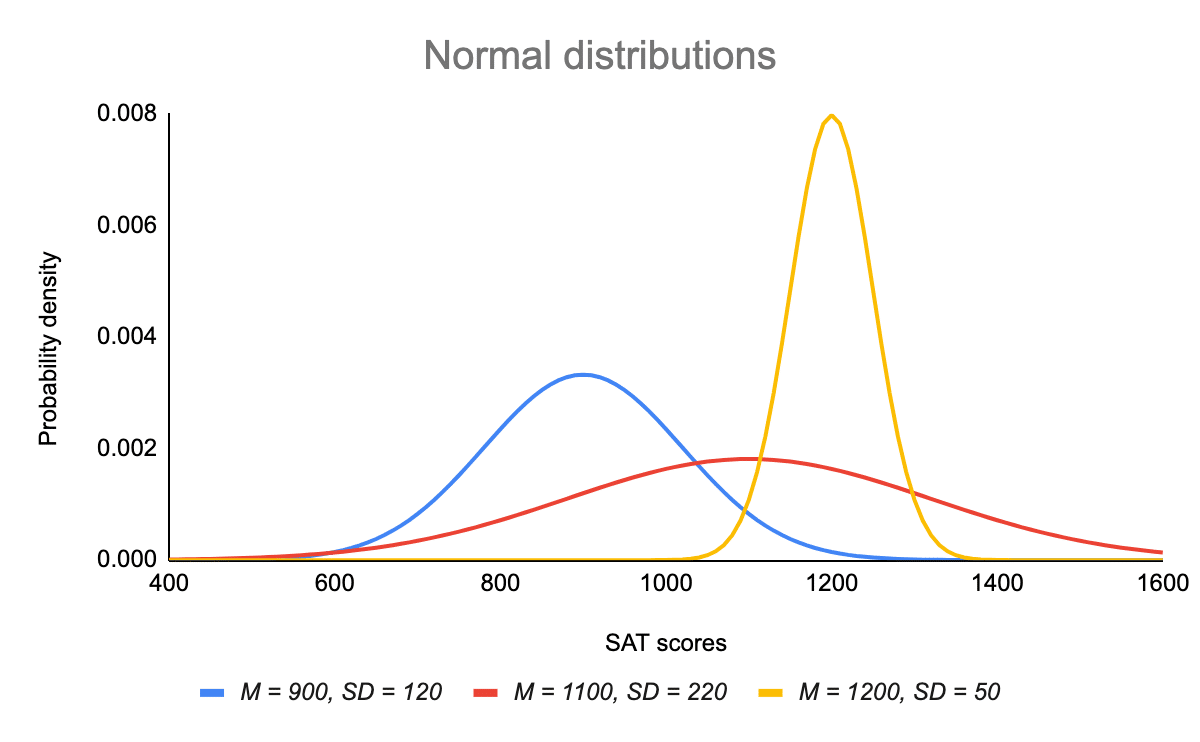
Normal Distribution Examples Formulas Uses

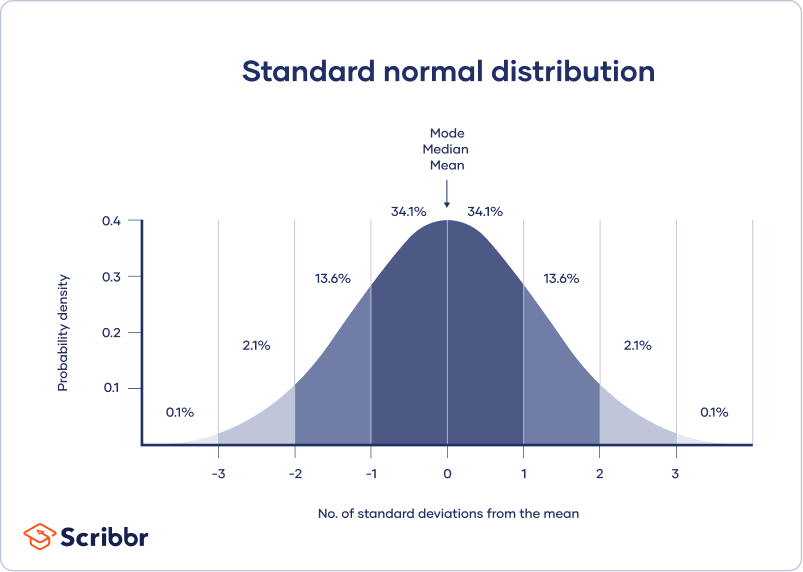
Normal Distribution Examples Formulas Uses

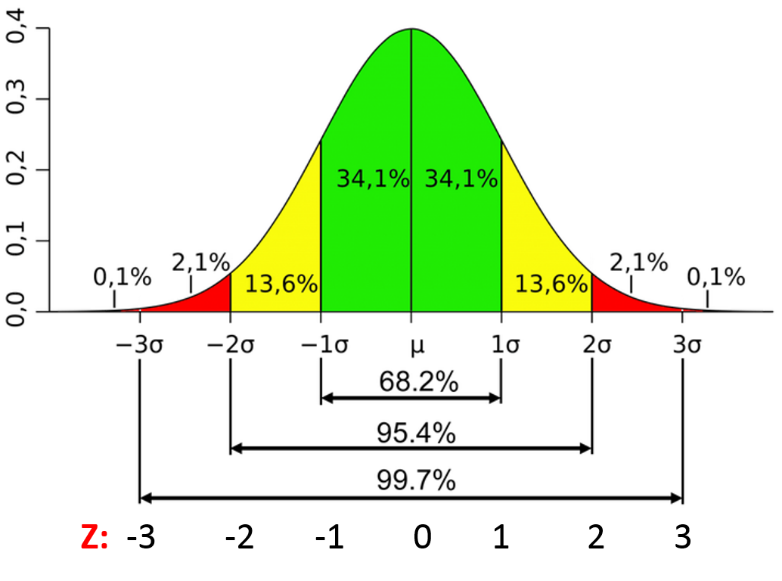
Characteristics Of A Normal Distribution

Normal Distribution The Statistics Matrix At Redbubble Sticker By Mark Stansberry Statistics Math Data Science Learning Math Methods

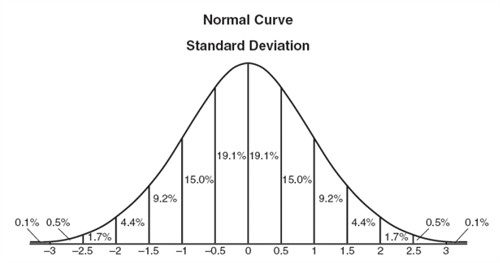
Standard Deviation And Normal Distribution Algebra 2 Quadratic Functions And Inequalities Mathplanet

Central Limit Theorem Sampling Distribution Of Sample Means Stats Probability Youtube

Normal Conditions For Sampling Distributions Of Sample Proportions Video Khan Academy

Standard Deviation A Step By Step Guide With Formulas

Nonparametric Statistics Data Is Not Required To Fit A Normal Distribution Nonparametric Statistics Uses Ordinal Statistics Math Data Science Research Methods

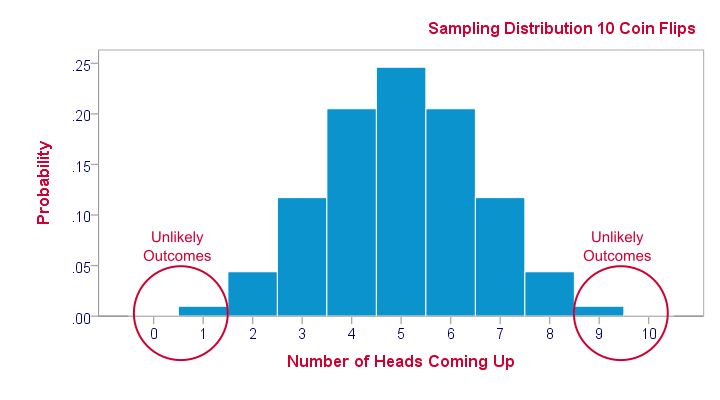
Sampling Distribution What Is It

Empirical Rule Definition

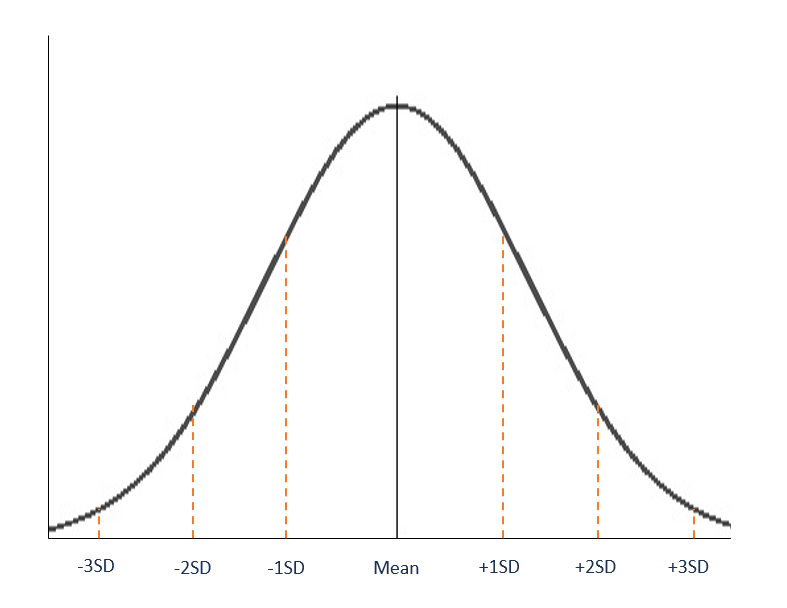
Normal Distribution Overview Parameters And Properties

T Distribution Definition

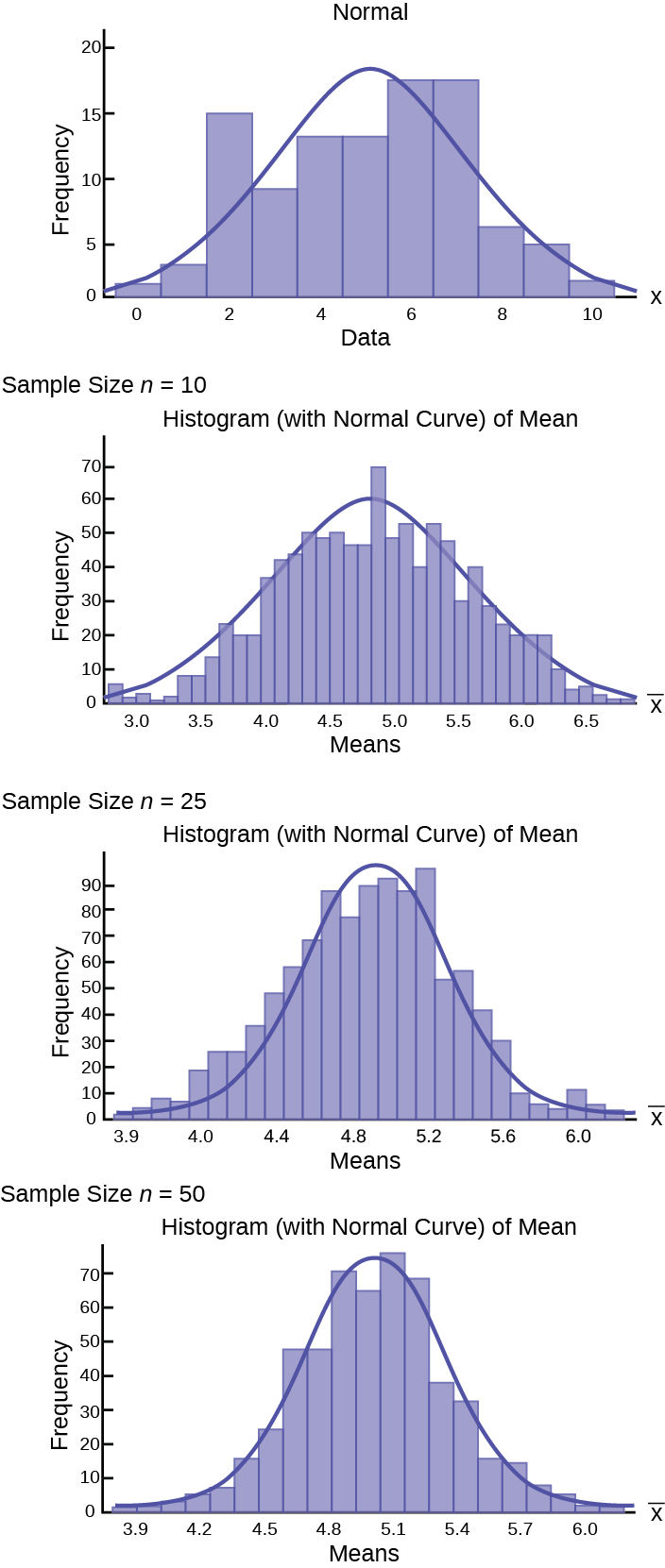
Using The Central Limit Theorem Introductory Business Statistics